Allgemeines oder schiefwinkliges Dreieck
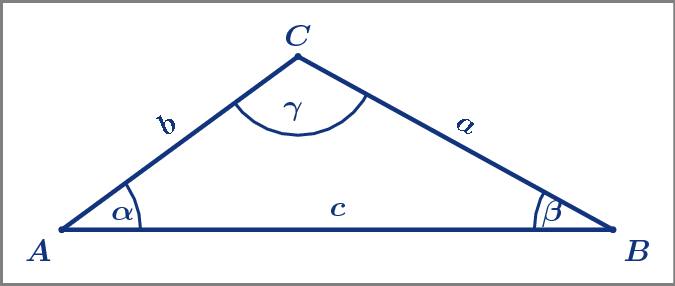
Wir benennen die Ecken, Seiten und Winkel wie üblich.
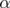 und gegenüber liegt
die Seite a; Der Eckpunkt B ist der Scheitel und so weiter.
und gegenüber liegt
die Seite a; Der Eckpunkt B ist der Scheitel und so weiter.
Das ist eine reine Festlegung, eine Konvention, an die Sie sich auch halten sollte, weil
es die Kommunikation vereinfacht. Andererseits: Namen sind nur Schall und Rauch –
es darf nichts davon abhängen, dass ich eine Seite c und nicht a genannt
habe, dass ich den a gegenüberliegenden Winkel mit 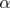 bezeichnet habe
...
bezeichnet habe
...
Anders als in einem rechtwinkligen Dreieck ist kein Winkel und damit auch kein Eckpunkt und keine Seite vor einer anderen ausgezeichnet. Insbesondere gibt es weder Hypotenusen noch Katheten.
Für rechtwinklige Dreiecke kennen wir den Satz von Pythagoras und seine Freunde, den Höhensatz und den Kathetensatz. zuständig. Die Welt der allgemeinen, schiefwinkligen Dreiecke dominieren die folgenden drei merkenswerten Sätze. Alles andere schlägt man bei Bedarf nach.
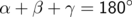
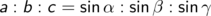
oder anders geschrieben
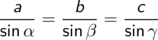
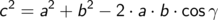
wobei der Winkel 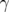 der Seite c gegenüberliegt. Anders ausgedrückt, der
Winkel
der Seite c gegenüberliegt. Anders ausgedrückt, der
Winkel 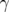 von den Seiten a und b eingeschlossen wird.
von den Seiten a und b eingeschlossen wird.
Da in einem schiefwinkligen Dreieck keine Seite vor den anderen ausgezeichnet ist, kann man völlig analoge Formeln für a und b aufschreiben – so ist die obige Formel zu verstehen.
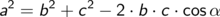
wobei der Winkel 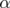 der Seite a gegenüberliegt.
der Seite a gegenüberliegt.

wobei der Winkel 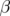 der Seite b gegenüberliegt.
der Seite b gegenüberliegt.
Allgemeine, schiefwinklige Dreiecke dürfen natürlich insbesondere auch rechtwinklig sein, sie müssen halt nur nicht.
Was wird in diesem Fall aus dem Kosinussatz?
Im rechtwinkligen Dreieck gibt es eine Hypotenuse, die wir wie üblich mit c bezeichnen.
Der ihr gegenüberliegende Winkel ist ein rechter, sein Kosinus demzufolge gleich Null. Damit reduziert sich der Kosinussatz zu
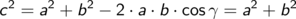
Guter, alter Pythagoras.
Der Kosinussatz ist der auf beliebige Dreiecke verallgemeinerte Satz von Pythagoras .
Von einem Dreieck sind die Seiten a = 6cm, c = 12 cm und der Winkel  = 23° bekannt.
Gesucht ist der Winkel
= 23° bekannt.
Gesucht ist der Winkel 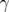 .
.
Lösung
Der Sinussatz
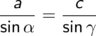
liefert

Wir kennen des Sinus des Winkels, also können wir unter Einsatz des Taschenrechners den Winkel berechnen

Wir haben eine Lösung übersehen.
Wie konnte das passieren? Schauen wir uns die Sache in Ruhe an:
Was lehrt uns das?
Beides sind wirklich Lösungen der Dreiecksaufgabe, da auch für den größeren der beiden Winkel noch etwas für den dritten Winkel übrig bleibt.