Im rechtwinkligen Dreieck heißt die dem rechten Winkel gegenüberliegende Seite Hypotenuse und wird mit c bezeichnet. Die beiden anderen Seiten, die den rechten Winkel einschließen, heißen Katheten .
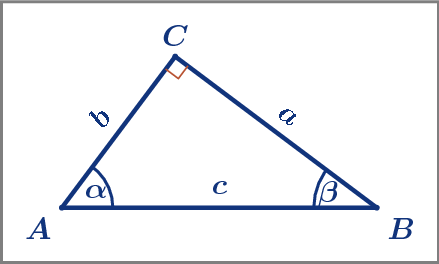
Beginnen wir mit dem wohl bekanntesten Satz der Schulmathematik, dem Satz von Pythagoras
Als Gleichung ausgedrückt
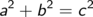
wobei a und b für die Längen der Katheten, c für die Länge der Hypotenuse steht.
Für beliebige Dreiecke ist der Satz von Pythagoras noch nicht einmal falsch; er ist einfach sinnlos, da es nur in rechtwinkligen Dreiecken überhaupt Katheten und eine Hypotenuse gibt.
Neben dem Satz von Pythagoras sind zwei weitere Sätze nützlich – zumindest sollte man wissen, dass es sie gibt, um sie dann bei Bedarf nachzuschlagen. (Oder herzuleiten: die Beziehungen folgen direkt aus der Ähnlichkeit der beiden Teildreiecke zueinander bzw. zum Gesamtdreieck.)
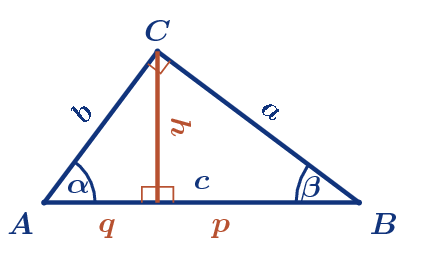
Der Fußpunkt der auf der Hypotenuse senkrecht stehenden Höhe des rechwinkligen Dreiecks teilt die Hypotenuse in zwei Hypotenusenabschnitte, die im Bild mit p und q bezeichnet sind.

wobei der Hypotenusenabschnitt p an der Kathete a anliegt und der Hypotenusenabschnitt q an der Kathete b.
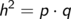
Die Summe der beiden nichtrechten Winkel beträgt 90°:
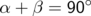
In typischen Aufgaben zur Dreiecksberechnung sind drei Bestimmungsstücke (Winkel, Seiten) gegeben, die fehlenden werden gesucht und müssen berechnet werden. Die notwendigen Beziehungen liefern die aufgeführten Sätze. Die Kunst ist, die jeweils passenden zu wählen, um sich die Arbeit so einfach wie möglich zu machen. Erfahrung hilft, es wird also immer besser.
Betrachten wir ein etwas anspruchsvolleres Beispiel mit eingebauten kleinen Tücken.
In einem rechtwinkligen Dreieck ist die Länge der einen Kathete a = 9 cm und des zur anderen Kathete gehörenden Hyptenusenabschnitts q = 12 cm gegeben. Zu bestimmen ist die Länge der Hypotenuse. Der Kathetensatz verbindet die bekannten und gesuchten Größen – wenn auch erst nachdem man p als c – q ausgedrückt hat:
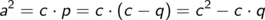
a und q sind bekannt, c ist gesucht.
Wie geht es weiter?
Mit der pq–Formel! Obwohl unser Hirn gerade im Geometriemodus arbeitet, erkennen wir, dass es sich um eine quadratische Gleichung zur Bestimmung von c handelt. Und merken uns gleich, dass c als Länge positiv sein muss.
Also auf Normalform bringen
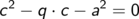
p und q ablesen und in die pq–Formel einsetzen.
An dieser Stelle werden wir unbarmherzig mit dem richtigen Leben konfrontiert: die Standard-Bezeichnungen aus der Geometrie und der Algebra kollidieren: Das q aus der Geometrie (der Hypotenusenabschnitt) darf nicht mit dem q aus der pq–Formel (dem Term ohne x) verwechselt werden. Wir müssen also ernsthaft mit der Bedeutung von p (Vorfaktor des in der gesuchten Größe linearen Terms) und q (Term ohne die gesuchte Größe) arbeiten. Das liefert die beiden Lösungen

Einsetzen der Werte liefert c1 = 16,82 cm. Die zweite Lösung der quadratischen Gleichung ist kleiner 0, also als geometrische Länge unbrauchbar.
Die Länge der Hypotenuse beträgt 16,82 cm.
Rechtwinklige Dreiecke treten nicht nur direkt, sondern auch, mehr oder minder gut versteckt, in anderen Figuren auf. Zum Abschluss deshalb noch eine Aufgabe, in der gleich zwei rechtwinklige Dreiecke die Hauptrolle spielen.
Bestimmen Sie in einem Würfel der Kantenlänge 4 cm den Winkel zwischen Flächen-
und Raumdiagonale.
Wie ändert sich der Winkel, wenn die Kantenlänge doppelt so groß ist?
Es gibt ein
Dreieck, das die Fächen- und Raumdiagonale enthält. Den Rest erledigt
Pythagoras.
Mit dem allgemeinen a lässt sich genau so schön rechnen, wie mit der konkreten 4.
aufgespannte rechtwinklige Dreieck.
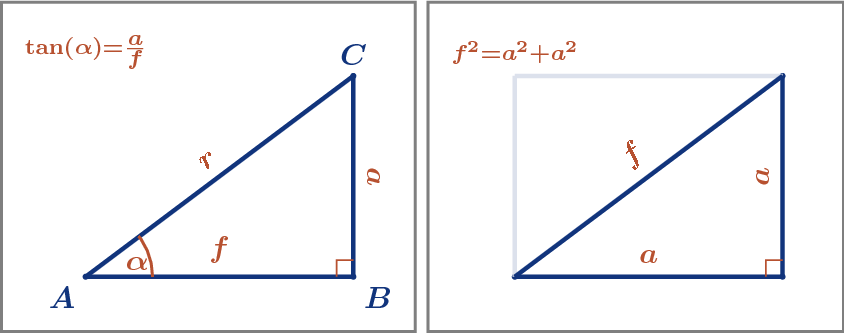
In diesem Dreieck ist die Raumdiagonale r des Würfels die Hypotenuse, die Flächendiagonale f des Würfels eine der Katheten und die hintere Würfelkante die andere Kathete. Der gesuchte Winkel ist also der Dreieckswinkel im Punkt A.
Damit ist das dreidimensionale Problem auf ein zweidimensionales plattgeklopft.
Die Länge der Flächendiagonale berechnen wir mit dem Satz von Pythagoras zu
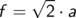
Damit kennen wir den Tangens des gesuchten Winkels zwischen Raum- und Flachendiagonale
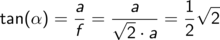
und somit den Winkel selbst
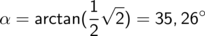
Kommen wir zur zweiten Frage: Der Winkel ist unabhängig von der Größe des Würfels. Die Kantenlänge ist bei der Rechnung herausgefallen.
Jenen, die mit einem guten geometrischen Vorstellungsvermögen gesegnet sind, war das vielleicht von Anfang an klar. Für alle anderen war es entscheidend, nicht gleich zu Anfang für die Kantenlänge a den Wert 4 eingesetzt zu haben.
Merke: Zusammenhänge lassen sich nur erkennen, wenn man erst am Ende konkrete Werte einsetzt.