Uneigentliche Integrale

Der Vollständigkeit halber sei noch an je einem Beispiel vorgeführt, wie die Definition des Integrals auf die Fälle ausgeweitet wird, in denen

• die Werte der zu integrierenden Funktion unbeschränkt wachsen, wie zum Beispiel in

  

• der Integrationsbereich sich ins Unendliche ausdehnt, wie zum Beispiel in

  

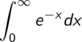
Man spricht in beiden Fällen von uneigentlichen Integralen und definiert sie als Grenzwert von “normalen” Integralen.

Unbeschränkter Integrand

Der Integrand divergiert im Nullpunkt.

Wir halten uns erst einmal von der kritischen Stelle fern, indem wir als untere Integrationsgrenze u statt 0 wählen.

Dieses (normale) Integral berechnen wir mithilfe einer Stammfunktion

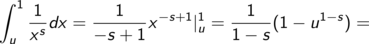
und bilden dann den Grenzwert für u gegen 0.

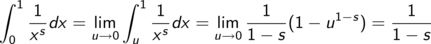
Die letzte Gleichheit gilt, da s kleiner 1 ist, also (1 - s) größer 0.

Unbeschränkter Integrationsbereich

In geometrischer Einkleidung fragen wir nach dem Flächeninhalt des unendlich langen Flächenstücks zwischen dem Graphen der Funktion e^-x und der positiven x-Achse.

Ist der Flächeninhalt überhaupt endlich?

Vielleicht schon: die Höhe der Fläche wird ja für große Werte von x sehr schnell fast Null . Wir haben also eine “Sehr viel von fast Nichts” Situation. Bei solchen Fragen hilft nur eins: Wir werden rechnen müssen.

Wir ersetzen die “kritische” unendliche obere Integrationsgrenze durch einen endlichen Wert, nennen wir ihn a.

Dieses (normale) Integral berechnen wir mithilfe einer Stammfunktion

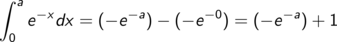
Im letzten Schritt lassen wir die obere Integrationsgrenze gegen unendlich gehen.

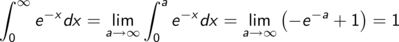
Fassen wir das Ergebnis in der geometrischen Einkleidung zusammen:
Der Flächeninhalt der unendlich langen Fläche zwischen dem Graphen der Funktion und der positiven x-Achse ist gleich dem des Quadrats mit der Seitenlänge 1.