Kompliziertere Integrale

Beim Ableiten halfen die Differentiationsregeln (Produktregel, Kettenregel etc.), um eine gesuchte Ableitung auf bekannte, tabellierte Ableitungen zurückzuführen.

Funktioniert das auch bei der Bestimmung von Stammfunktionen?
Da die Integration die Umkehrung der Differentiation ist, gibt es doch zu jeder Differentiationsregel eine entsprechende Integrationsregel!

Leider nicht wirklich.
Zwar gibt es die den Differentiationsregeln entsprechenden Integrationsregeln (partielle Integration, Integration durch Substitution etc.) – aber zu wissen, wann man welche Regel wie anwenden muss, ist beim Integrieren schwierig, oft trickreich, meist aufwändig.

Computeralgebrasysteme sind nützliche Helfer

Deshalb ist heute ein Computeralgebrasystem wie Maxima das Werkzeug der Wahl wenn es gilt, etwas kompliziertere Stammfunktionen zu bestimmen oder anspruchsvollere Integrale zu berechnen.

Maxima Beispiele

In dem Computeralgebrasystem Maxima können wir Stammfunktionen und Integrale mit dem Befehl (der Maximafunktion) integrate berechnen.

Stammfunktion

integrate(sin(x)^3, x)

erweist

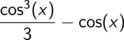
als eine Stammfunktion von sin³(x).

Integral

integrate(cos(x)^2 * exp(x), x, 0, %pi)

berechnet

Uneigentliches Integral

integrate(x ^ 2 * exp(-x ^ 2), x, minf, inf)

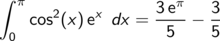
liefert

Etwas Kopfarbeit schadet auch nicht

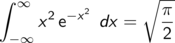
Linearität Wegen der Linearität des Differenzierens (und da man als unbedarfter Anwender dazu neigt, alles für additiv zu halten) überraschen die folgenden Regeln nicht

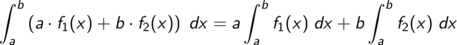
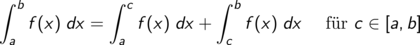
Insbesondere können wir wegen der ersten Regel alle Polynome “im Kopf” integrieren.

Beispiel

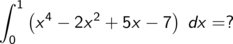
Wegen der Linearität im Integranden folgt

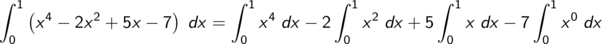
Die kleine Tabelle der wichtigsten Stammfunktiuonen liefert

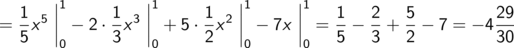
Manchmal hilft eine offensichtliche Substitution Nämlich dann, wemn Sie für ein ganz ähnliches Problem die Lösung bereits kennen.

Einfaches Beispiel zur Substitutionsregel

Wir suchen den Wert des Integrals

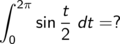
und kennen aus der Tabelle das Integral

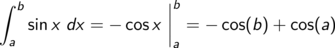
Es bietet sich an, zu einer neuen Variablen x = t/2 überzugehen, zu substituieren.

Wir müssen dann aber auch das “Differential” dx und die Integrationsgrenzen umrechnen.

Variable

Differential

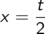
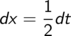
Eine (Längen-)Änderung in t bewirkt eine halb so große Änderung in x

Integrationsgrenzen

Alles eingesetzt und fertig

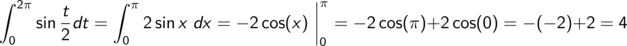
Substitution ist ein Prinzip, das sich auch in anderen Zusammenhängen (Gleichungen, Differentialgleichungen) bewährt. Denken Sie zum Beispiel an die biquadratischen Gleichungen. Dahinter steht immer die Hoffnung, dass in der neuen Variablen alles besser aussieht.