So wie wir Ableitungen nicht als Grenzwert von Differenzenquotienten berechnet haben, wollen wir auch den Wert eines Integrals nicht mühsam dadurch bestimmen, dass wir mit Treppenfunktionen, Summen und Grenzwerten hantieren.
Brauchen wir auch nicht. Denn es gibt Stammfunktionen und ihren unmittelbar aus dem Hauptsatz folgenden Zusammenhang mit Integralen.
Stammfunktion einer auf einem Intervall D stetigen Funktion f wird eine differenzierbare Funktion F genannt, deren Ableitungsfunktion F’ mit f übereinstimmt
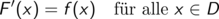
Ist f eine stetige reellwertige Funktion auf einem Intervall D und F eine Stammfunktion von f, so gilt
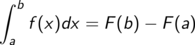
für alle a, b aus dem Intervall D.
Kenne ich eine Stammfunktion F von f, kann ich alle Integrale über den Integranden f berechnen. Einfach als Differenz der Funktionswerte der Stammfunktion an der oberen und unteren Integrationsgrenze.
Un woher bekomme ich eine Stammfunktion des Integranden? Etwa durch Integrieren? Ja schon, aber halt auch anders. Zum Beispiel indem ich die Tabelle der Ableitungen der wichtigsten Funktionen “gegen den Strich” lese!
Potenzfunktionen
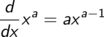
Exponentential- und Logarithmus-Funktion

Für a > 0:
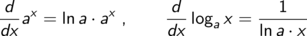
Trigonometrische Funktionen
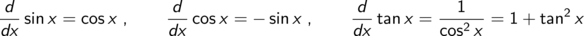
Bogenfunktionen
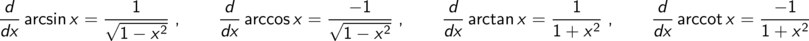
Ich suche nicht nach der Ableitung einer Funktion, sondern ich kenne die Ableitung (den Integranden) und suche umgekehrt eine (Stamm-)Funktion.
Beachte: Im englischen Sprachraum wird das bereits in den Bezeichnungen deutlich: Ableitung = derivative, Stammfunktion = antiderivative.
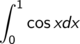
Ein Blick zurück in die Übersicht der wichtigsten Funktionen und ihrer Ableitungen zeigt, dass der Sinus eine Stammfunktion des Cosinus ist, also
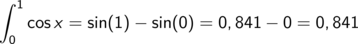
Wie gewünscht, haben wir das Integral ohne Summen- und Grenzwertbildung berechnet.
Sie müssen das Integral
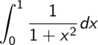
berechnen, brauchen also eine Stammfunktion des Integranden.
Die Befragung eines Mitstudenten, einer klassischen Formelsammlung und googeln liefert drei unterschiedliche Antworten: Die Stammfunktion sei
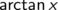
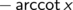
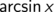
Welche Stammfunktion nehmen Sie? (Es sind nur mathematische, keine medienkritischen Begründungen erlaubt) Denken Sie einfach an die Definition einer Stammfunktion
Ein Blick in den Abschnitt Bogenfunktionen der Tabelle der wichtigsten Ableitungen
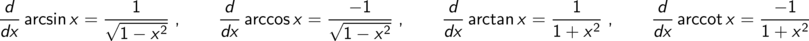
zeigt, dass sowohl der erste Kandidat als auch der zweite Stammfunktionen sind, der dritte aber nicht.
Wir wählen den Arkustangens als Stammfunktion und berechnen das Integral
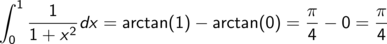
Genausogut hätten wir den mit minus 1 verzierten Arkuscotangens als eine Stammfunktion verwenden können.
Das Ganze ist schon etwas überraschend: Wir wissen zwar, das eine Stammfunktion nicht eindeutig ist, sondern das die Addition einer Konstanten wieder eine Stammfunktion ergibt. Nur das die so erhaltene Stammfunktion sogar einen anderen Namen haben kann, hatten wir vielleicht doch nicht auf der Rechnung.
Merkenswert: Das zwei Funktionen sich nur um eine additive Konstanten unterscheiden, sieht man ihnen nicht immer auf den ersten Blick an.
Ja, und. auf der Seite Integrale in der Physik haben wir das im Abschnitt Änderungsraten summieren auch schon gemacht
Hier noch einmal in anderen Worten:
Wir schreiben den Hauptsatz als “Integralformel” um, die den Wert einer stetig differenzierbaren Funktion F an einer beliebigen Stelle t durch den Anfangswert t0 und ihre Ableitung ausdrückt
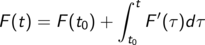
Interpretieren wir die Variable t als Zeit und erinnern uns daran, dass die Ableitung F’ der Änderungsrate entspricht, liest sich diese Formel wie folgt: Der Wert einer Größe F zum Zeitpunkt t ist gleich ihrem Anfangswert plus den aufsummierten Änderungen.
.