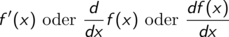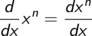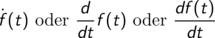Ableitung als Funktion
Definition
Ist eine Funktion an jeder Stelle ihres Definitionsbereichs differenzierbar, so nennt
man f eine differenzierbare Funktion.
Für differenzierbare Funktionen erhält man durch Differenzieren eine neue Funktion,
die Ableitung , die jeder Stelle des Definitionsbereichs die Ableitung der Funktion an
dieser Stelle zuordnet.
Notation Die Ableitung der Funktion f bezeichnet man mit
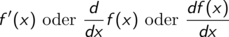
Beispiel

Die alternativen Schreibweisen können auch für namenlose, anonyme, Funktionen
verwendet werden.
Beispiel
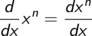
Wenn das Argument von f die Zeit ist, bietet sich als Bezeichnung t anstelle von x
an. In diesem Fall wird die Ableitung nicht mit einem Strich, sondern mit einem
Punkt symbolisiert. Beispiel
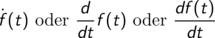
Höhere Ableitungen
Wenn(!) die Ableitung einer Funktion f selbst wieder
differenzierbar ist, so lässt sich die zweite Ableitung von f als Ableitung der ersten
definieren. Nach dem selben Schema (Wenn – Dann) können auch dritte, vierte etc.
Ableitungen definiert werden.
Speziell die zweite Ableitung kommt auch in den Anwendungen häufig vor.
-
Physik
- Die erste Ableitung des Ortes liefert die (Momentan-) Geschwindigkeit.
Die zweite Ableitung beschreibt also die Änderungsrate der momentanen
Geschwindigkeit, vulgo die momentane Beschleunigung.
-
Politik
- Wenn die Aussage der ersten Ableitung über die Entwicklung der
Verschuldung “Die Schulden sind gewachsen” nicht genehm ist, hilft ja
vielleicht der Griff zur zweiten Ableitung “Es ist gelungen, das Wachstum
der Schuldenzunahme zu verringern.”
Hört sich schon viel besser an.
Graphen, Graphen, Graphen
Das Ganze am besten in einfachen Bildern; also muss
die quadratische Funktion wieder einmal herhalten.
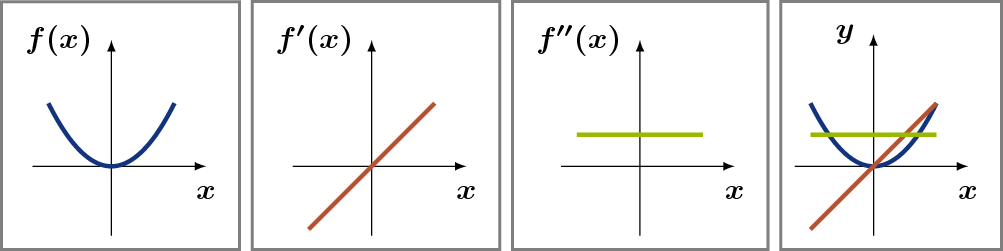
An den Graphen lesen wir ab:
-
Erste Ableitung: Steigung
- Die erste Ableitung beschreibt die Änderung der
Funktionswerte an der jeweiligen Stelle, also die Steigung des Graphen in
den entsprechenden Punkten.
Wir sehen, dass für positive x-Werte die Steigung größer Null ist, das heißt
die Funktion wächst. Und zwar um so stärker, je größer x ist (da die erste
Ableitung mit x wächst).
-
Zweite Ableitung: Krümmumg
- Die zweite Ableitung
beschreibt die Änderung der Funktionswerte der ersten Ableitung, also die
Änderung der Steigung. Geometrisch gesprochen ist das die Krümmung
des Funktionsgraphen.
In unserem einfachen Beispiel ist die Krümmung in allen Punkten gleich.