Rechnen mit Funktionen

Mit Funktionen können Sie rechnen, und zwar genauso wie mit reellen Zahlen.

Die algebraischen Rechenoperationen

lassen sich auf natürliche, naheliegende Weise von den reellen Funktionswerten auf die Funktionen als Ganzes übertragen

Natürlich bedeutet in diesem Zusammenhang, dass die Mathematiker alles so definieren, wie Sie es auch täten (wenn Sie die Notwendigkeit einer Definition einsähen).

Fragen wir uns als:

Was soll die Summe zweier Funktionen f und g (mit gleichem Definitionsbereich D) sein? Kurzform: Funktionswerte addieren.

Definition der Summenfunktion:

Die Summe zweier Funktionen f und g ist selbst wieder eine Funktion f + g

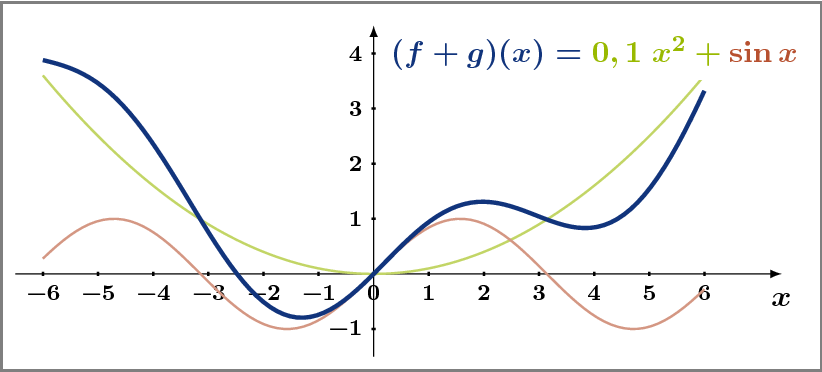
FORMEL

FORMEL

Erkennen Sie die punktweise Addition der Funktionswerte? Betrachten Sie zum Beispiel die Summenfunktion an den Nullstellen der Sinus-Funktion.

Zusatzfrage:

Was ist, wenn die Definitionsbereiche nicht gleich sind? Wenn an einer Stelle nur eine Funktion definiert ist, gibt es auch nur einen Funktionswert, also ...

Antwort:

Nun, dann ist die Summenfunktion nur auf der Schnittmenge der Definitionsbereiche definiert – der im Extremfall leer ist.
Nach dem gleichen Schema definieren wir die Multiplikation zweier Funktionen.

Multiplikation von Funktionen

Das Produkt zweier Funktionen f und g ist selbst wieder eine Funktion f g

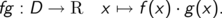
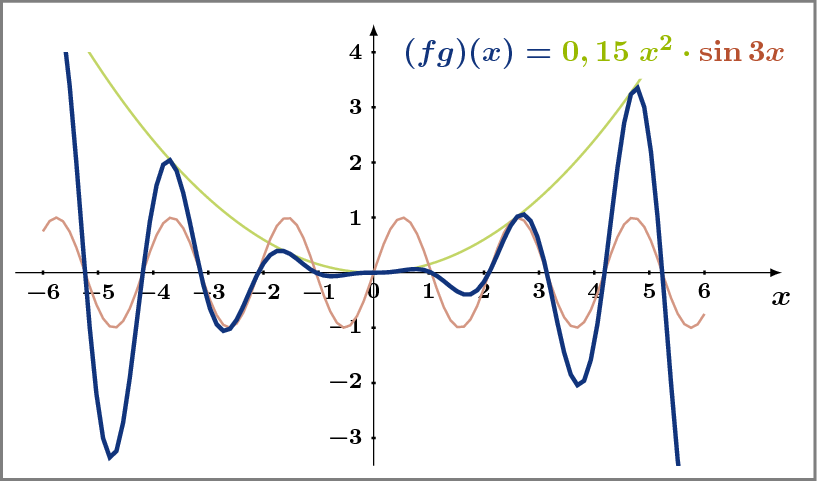
FORMEL

FORMEL

Erkennen Sie die punktweise Multiplikation der Funktionswerte? Betrachten Sie zum Beispiel die Produktfunktion an den Nullstellen der Sinus-Funktion.

Falls g nirgends auf dem Definitionsbereich den Wert 0 annimmt, ist auch der Quotient f/g über die Multiplikation mit dem Kehrwert definiert. Notfalls hilft die Enschränkung des Definitionsbereichs. Denken Sie an die Definition der Tangensfunktion als Quotient der Sinus- und Kosinusfunktion.

Beispiele

Vornehm ausgedrückt, können wir mit Funktionen Algebra betreiben.
Pragmatisch gesehen, können wir bereits bekannte Funktionen als Bausteine verwenden und daraus neue Funktionen konstruieren. Und davon wird ausgiebig Gebrauch gemacht.

Wir beschränken uns hier zunächst auf Schlagworte.