Quadratische Gleichungen: Herleitung der pq

Mancher, der sich die pq–Formel nicht merken kann, hat mit der quadratischen Ergänzung schneller eine quadratische Gleichung zu Fuß gelöst als die Formel nachgeschlagen.

Beispiel

Gesucht sind alle reellen Lösungen der Gleichung

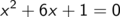
Wir bringen den Term ohne x auf die andere Seite

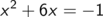
und addieren dann auf beiden Seiten das Quadrat des halben Vorfaktors des linearen Terms, die sogenannte quadratische Ergänzung. Der Vorfaktor des linearen Terms ist 6, die quadratische Ergänzung, das Quadrat des halben Vorfaktors, also 3²

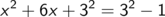
Wegen der binomischen Formel (a + b)² = a² + 2 a b + b² (von rechts nach links gelesen) folgt

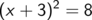
und daraus

Beweis der pq–Formel

Wir haben im obigen Beispiel die pq–Formel für einen konkreten Einzelfall hergeleitet.

Den allgemeinen Beweis der pq–Formel für beliebige Werte der Parameter p und q können Sie völlig analog führen. Wem es also Spass macht, der lese weiter (oder versuche es nach obigem Muster erst einmal selbst).

Der Beweis

Ausgangspunkt ist die quadratische Gleichung

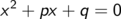
Wir bringen den Term ohne x auf die andere Seite

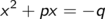
und addieren dann auf beiden Seiten die quadratische Ergänzung (p/2)²

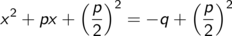
Wegen der binomischen Formel (a + b)² = a² + 2 a b + b² steht durch diesen Kunstgriff auf der linken Seite ein reines Quadrat, nämlich das der Summe x + p/2

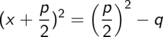
Das Quadrat von x + p/2 ist gleich (p/2)² – q, also muss

sein. Beachten Sie die beiden Vorzeichen.

Jetzt müssen wir nur noch p/2 auf die andere Seite bringen und die pq–Formel steht da.

Der letzte Schritt bei dem die Wurzel mit den beiden Vorzeichen auftrat ist ziemlich hingeschlampert, also zur Sicherheit noch einmal etwas langsamer.

Das Detail

Ausganspunkt ist die Gleichung

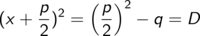
wobei wir wieder die Diskriminante D = (p/2)² – q eingeführt haben. Wir machen eine Fallunterscheidung:

Fall D < 0

Die rechte Seite ist negativ, die linke Seite das Quadrat einer reellen Zahl, also immer positiv.

In diesem Fall gibt es offensichtlich keine reelle Lösung.

Fall D >= 0

In diesem Fall sind beide Seiten der Gleichung positiv. Deshalb können wir die Wurzel ziehen ohne die Lösungsmenge zu ändern. (Zwei positive Zahlen sind genau dann gleich, wenn ihre Wurzeln gleich sind.)

Aber Achtung: Die Wurzel aus dem Quadrat einer beliebigen (also unter Umständen negativen) Zahl ist nicht die Zahl selbst, sondern deren Betrag (der ist nämlich wie die Wurzel immer positiv). Also

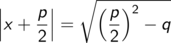
und damit

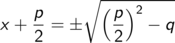
Womit wir uns den kritischen Schritt zumindest einmal sorgfältig überlegt haben.