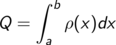Integrale in der Physik
Integrale sind Grenzwerte von Summen (einfach zu berechnender Summanden)
Integrale treten immer dann auf, wenn man (unendlich) viele (verschwindend) kleine
Beiträge aufsummieren muss.
Solche Summationen kommen in der Physik häufig vor, da auch dort, wie bei der
Flächenberechnung, die sehr kleinen Beiträge relativ leicht zu bestimmen
sind.
Konkret: Zurückgelegte Strecke berechnen
Welche Wegstrecke legt ein Massepunkt
zurück, der sich mit variabler, zeitabhängiger Geschwindigkeit auf einer Geraden
bewegt?
-
Einfacher Fall: Konstante Geschwindigkeit
- Beginnen wir mit dem (nicht
gefragten) einfachen Fall konstanter Geschwindigkeit:
Bei konstanter Geschwindigkeit v0 legt der Massepunkt in einem
Zeitintervall der Dauer  die Strecke
die Strecke
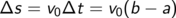
zurück.
-
Summe: Geschwindigkeit auf kurzen Zeitintervallen näherungsweise konstant
-
Bei zeitabhängiger Geschwindigkeit verfahren wir nach der Methode “teile
und herrsche”. Wir zerlegen das Zeitintervall so in kleine Teilintervalle
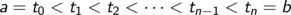
dass die Geschwindigkeit auf
den Teilintervallen 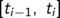 näherungsweise den konstanten Wert vi
hat.
näherungsweise den konstanten Wert vi
hat.
In dieser Näherung erhalten wir die zurückgelegte Strecke als Summe
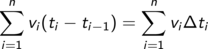
Dabei steht  für die Dauer des kleinen Zeitintervalls.
für die Dauer des kleinen Zeitintervalls.
-
Grenzwert: Die Näherung wird exakt
- Im Grenzwert immer kürzerer
Teilintervalle, auf denen die Geschwindigkeit dann “wirklich”, und nicht
nur halbwegs, konstant ist, erhalten wir den zurückgelegten Weg bei
zeitabhängiger Geschwindigkeit

Allgemein: Änderungsraten summieren
Wir haben im ersten Beispiel aus dem
vorgegebenen Geschwindigkeitsverlauf, der zeitabhängigen Änderungsrate des Weges,
die insgesamt zurückgelegte Wegstrecke als Integral bestimmt.
Diese Vorgehensweise lässt sich auf eine beliebige zeitabhängige Größe G
übertragen.
Wir kennen die Änderungsrate g von G und fragen nach der Änderung der Größe G in
dem Zeitintervall von t1 bis t2.
-
Einfacher Fall: Konstante Änderungsrate
- Bei konstanter Änderungsrate
erhalten wir die Änderung der Größe durch Multiplikation der
Änderungsrate mit der Länge des Zeitintervalls
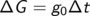
-
Summe: Änderungsrate auf kurzen Zeitintervallen näherungsweise konstant
-
Bei zeitabhängiger Änderungsrate zerlegen wir das Zeitintervall in kleine
Teilintervalle, auf denen die Änderungsrate näherungsweise konstant ist
und erhalten
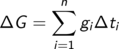
-
Grenzwert: Die Näherung wird exakt
- Im Grenzwert immer kürzerer
Teilintervalle erhalten wir für die Änderung von G im Zeitintervall
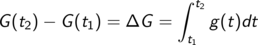
Stark verkürzt, aber hoffentlich verständlich: Die Differenz von Endwert und
Anfangswert der Größe erhalte ich durch Aufsummieren / Aufintegrieren ihrer
Änderungen in der Zeit dazwischen.
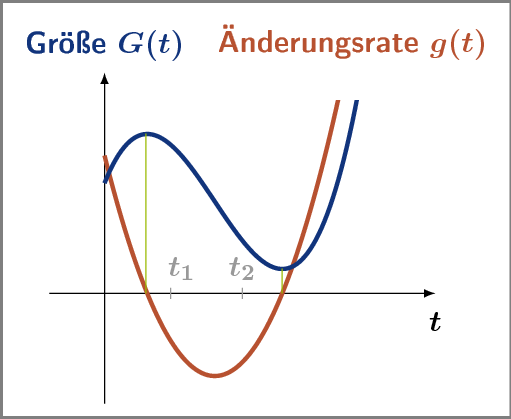
Im Bild sehen Sie den Verlauf der Größe G und ihrer Änderungsrate g .
Das Bild ist einen zweiten Blick wert:
Aufgabe:
Bringen Sie für die beiden eingezeichneten Zeiten t1 und t2
Achten Sie auf das Vorzeichen der beiden beiden Größen.
Beide Größen
sind negativ, Streckenlängen und Flächeninhalte immer positiv.
Antwort:
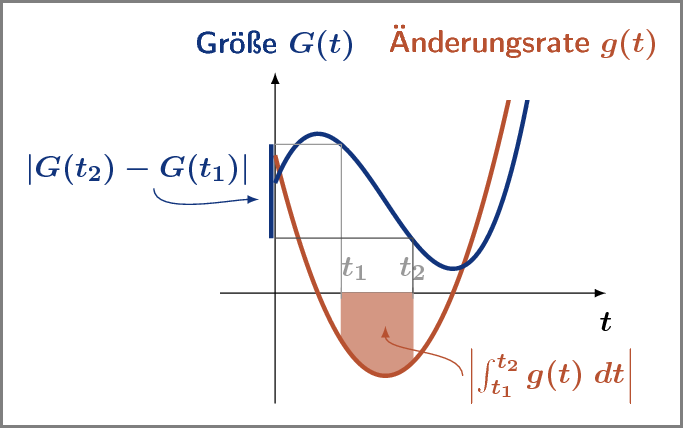
Das Bild liefert die Anwort – und wirft die nächste Fragen auf: Warum braucht man
die Beträge?
- Die Änderungsrate g ist in dem betrachteten Zeitintervall immer negativ.
- Die Funktion G fällt deshalb in dem gesamten betrachteten Zeitintervall,
die Differenz von Endwert und Anfangswert ist kleiner Null.
- Also ist die positive Streckenlängen gleich dem Betrag der Differenz, nicht
gleich der Differenz selbst.
Gleiches gilt für das Integral als gewichtete Flächeninhalt. Gewichtet bedeutet
nämlich, das Flächen unterhalb der t-Achse negativ zählen.
Spätestens jetzt versteht man, warum es sinnvoll war, das Integral als gewichteten
Flächeninhalt zu definieren. (Auch wenn es die Flächenberechnung unter
Umständen umständlicher macht.) Nur deshalb stimmt nämlich der obige,
physikalisch so gut verständliche, Zusammenhang zwischen Integral und
Änderungsrate.
Analog: Dichten integrieren
Die folgende Aufgabe lässt sich analog zu den Beispielen
lösen – diese Floskel verheißt nur selten Gutes.
Frage:
Wie groß ist die Ladung eines geraden Drahtes der Länge l mit bekannter
(Linien-)Ladungsdichte 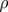 ?
Die 1-dimensionale Ortskoordinate x übernimmt die
Rolle der Zeit t
?
Die 1-dimensionale Ortskoordinate x übernimmt die
Rolle der Zeit t
Antwort:

-
Einfacher Fall: Homogene Ladungsdichte
- Bei homogener, das heißt
konstanter, Ladungsdichte
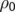 ist die Gesamtladung Q
ist die Gesamtladung Q

-
Summe: Ladungsdichte auf kurzen Intervallen näherungsweise konstant
-
Bei einer inhomogenen, ortsabhängigen Ladungsdichte unterteilen wir den
Draht in kleine Segmente, auf denen die Ladungsdichte näherungsweise
konstant ist.

-
Grenzwert: Die Näherung wird exakt
- Im Grenzwert immer kürzerer
Intervalle wird die Näherung exakt und die Summe geht in das Integral
über.
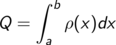
 die Strecke
die Strecke
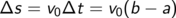
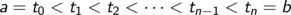
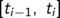 näherungsweise den konstanten Wert vi
hat.
näherungsweise den konstanten Wert vi
hat.
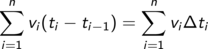
 für die Dauer des kleinen Zeitintervalls.
für die Dauer des kleinen Zeitintervalls.


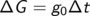
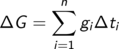
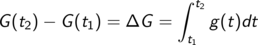


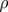 ?
Die 1-dimensionale Ortskoordinate x übernimmt die
Rolle der Zeit t
?
Die 1-dimensionale Ortskoordinate x übernimmt die
Rolle der Zeit t 
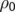 ist die Gesamtladung Q
ist die Gesamtladung Q