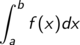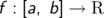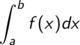Integrale: Grundidee und Definition
Nach der Untersuchung des Verhaltens von Funktionen im Kleinen, der
Differenzialrechnung, richten wir den Blick auf das große Ganze, die Fläche unter
dem Funktionsgraphen. Willkommen bei der Integralrechnung.
Die anschauliche, geometrische Bedeutung des Integrals (so es denn existiert)
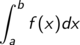
einer Funktion f von a (der unteren Integrationsgrenze) bis b (der oberen
Integrationsgrenze) ist der Flächeninhalt unter dem Graphen der Funktion im
Intervall [a, b].
Die Definition von Flächeninhalten krummlinig berandeter Flächen stellt man sich
am Besten als Dreisprung vor:

-
Einfacher Baustein
- Man startet von sicherem Terrain. Der Flächeninhalt
eines Rechtecks ist das Produkt seiner Seitenlängen.
-
Summe
- Um darauf aufzubauen, nähert man die Funktion durch (stückweise
konstante) Treppenfunktionen an. Den Flächeninhalt unter dem Graphen
einer Treppenfunktion kann man als Summe von Rechteckflächen leicht
berechnen, und erhält so eine Näherung des gesuchten Flächeninhalts.
-
Grenzwert
- Durch immer bessere Näherung, immer mehr, immer schmalere
Treppenstufen, erhält man im Grenzwert (unendlich vieler verschwindend
kleiner Einzelbeiträge) den Flächeninhalt unter dem Graphen der
Funktion
Der mathematische Aufwand, diese Schritte zu präzisieren, ist (für uns zu) hoch und
bleibt den Mathematikern überlassen. Die Vorteile nutzend, die Diebstahl gegenüber
ehrlicher Arbeit hat (selbst das Zitat ist geklaut), fassen wir deren Arbeit zusammen
und halten fest:
Definition und Satz
Jede stetige Funktion
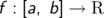
ist integrierbar, das heißt das Integral
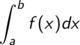
existiert und stellt den gewichteten Flächeninhalt unter dem Graphen der Funktion
dar.
Integrale berechnen den gewichteten Flächeninhalt, das heißt Beiträge unterhalb
der x-Achse zählen negativ.
Mit den stetigen Funktionen haben wir bereits einen erfreulich großen Vorrat an
integrierbaren Funktionen. Darüber hinaus können auch nichtstetige Funktionen
integrierbar sein. Zum Beispiel Funktionen mit endlich vielen Sprungstellen endlicher
Höhe.
Wir kümmern uns als nächstes darum, warum Integrale, also Grenzwerte von
Summen, in den Anwendungen wichtig sind und wie man sie berechnet. Neugierige
können zuvor noch einen kurzen Blick in die mathematische Werkstatt werfen, in der
die Herren Riemann und Lebesgue bei der Arbeit sind.
Arbeit für die Mathematiker
-
Was ist zu tun?
-
- Existiert der Grenzwert überhaupt und ist er unabhängig von den
Einzelheiten der Unterteilung, der Wahl der Treppenfunktionen?
- Für welche Funktionen und Integrationsbereiche?
- Welche Regeln gelten für den Umgang mit Integralen?
-
Wie wird es getan?
-
- Herr Riemann hantiert ganz klassisch mit den aus der Schule
bekannten Unter- und Obersummen.
- Herr Lebesque, ein Moderner, unterteilt dagegen die Funktionswerte
auf der y-Achse und summiert die Maße der x-Bereiche auf, die zu
den verschiedenen Funktionswerten gehören.
-
Was kommt raus?
-
- Die beiden Herren stimmen zwar nicht in jedem Einzelfall überein, ob
eine Funktion über einem Intervall integriebar ist, aber fast immer.
Dann erhalten sie auch den gleichen Wert für das Integral.
Technischen Anwendungen, die darauf beruhen, dass eine Funktion
Lebesgue- aber nicht Riemann-integrierbar ist, sollte man –
zurückhaltend formuliert – mit einer gehörigen Portion Skepsis
begegnen.
- Herr Lebesgue hat schönere Regeln für den Umgang mit seinen
Integralen, musste vorher aber auch härter arbeiten. Er kennt nicht
nur die üblichen Regeln, wie zum Beispiel die Substitutionsregel,
sondern darf auch Grenzprozesse vertauschen. Physiker durften das
schon immer (Warum soll ich das nicht dürfen???).