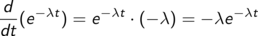Ableitungs-Regeln

Mit der Tabelle der Ableitungen wichtiger Funktionen alleine kommt man nicht aus. Die nächste Stufe ist, eine gesuchte Ableitung auf eine bekannte, tabellierte Ableitung zurückzuführen.

Konkret: Sie suchen die Ableitung von 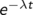, die Tabelle liefet aber nur die Ableitung von e^x. Das sieht machbar aus, und ist es auch, wenn wir eine, die passende, Regel zum Rechnen mit Ableitungen anwenden.

Die wichtigsten Regeln für zwei differenzierbare Funktionen f und g und eine Konstante a lassen sich kurz und knapp zusammenfassen.

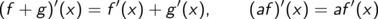
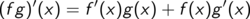
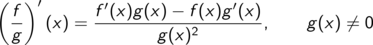
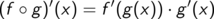
Diese Kurzform ist als Merkregel gefasst, nicht als mathematischer Satz. Unter den Teppich gekehrt wurde die Frage, ob die zusammengebauten Funktionen (Summe, Produkt, ...)

• überhaupt definiert sind: Das ist eine Forderung an die Definitionsbereiche, die zusammenpassen müssen. Das heißt in den meisten Fällen, dass sie gleich sein müssen, bei der Kettenregel aber, dass das Bild von f im Definitionsbereich von g liegt.
• wieder differenzierbar sind, die Berechnung der Ableitung also überhaupt sinnvoll ist. Das muss in der Mathematik ordentlich bewiesen werden.

Die Regeln sind bereits aus der Schule vertraut, oder zumindest bekannt. Das Problem sind also weniger die Regeln als ihre souveräne Anwendung.

Wir müssen lernen, im konkreten Fall die Struktur (Summe, Produkt, Verkettung) zu erkennen, um f und g abzulesen – und das erfordert etwas Übung.

Deshalb, und da das Erkennen von Strukturen nichts prinzipiell Schlechtes ist, folgt ein kurzes Frage – Antwort Spiel.

Beispiele

Linearität

Berechne:

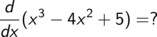
Ohne Worte

Lösung:

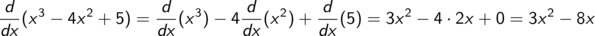
Auf diese Weise können Sie beliebige Polynome problemlos ableiten.

Produktregel

Berechne:

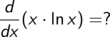
Ableitung von ln steht in der Tabelle

Lösung:

Quotientenregel

Berechne:

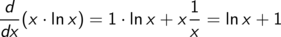
sin² x plus cos² x gleich 1

Lösung:

Kettenregel

Berechne:

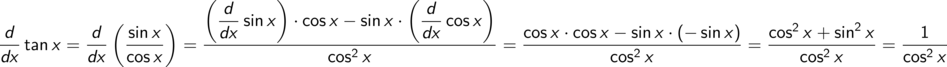
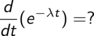
Nachdifferenzieren: Äußere Ableitung mal innere Ableitung

Lösung:

Zuerst müssen wir die Bausteine der zusammengesetzten Funktion erkennen:

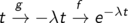
Anwendung der Kettenregel, also äußere Ableitung mal innere Ableitung, liefert