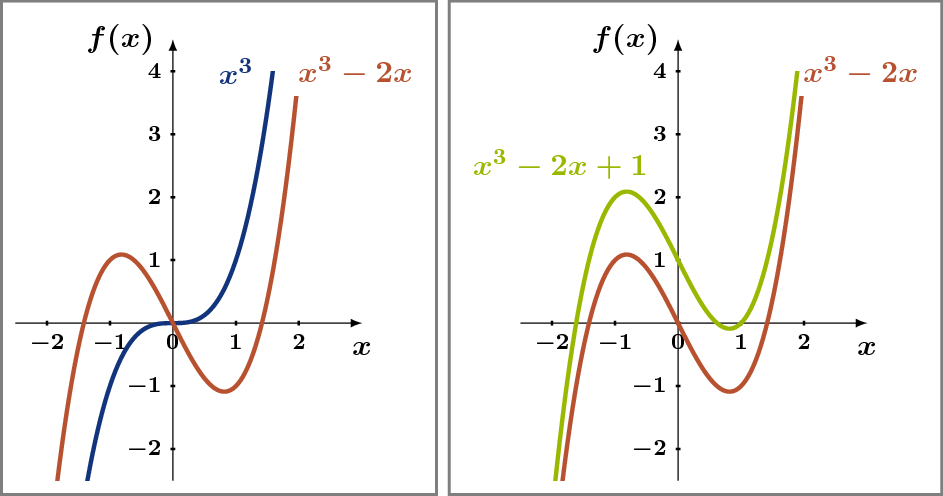
Bisher haben wir Funktionen analytisch durch die Angabe einer Vorschrift zur Berechnung der Funktionswerte beschrieben.
Sehr nützlich, weil anschaulich, ist die bildhafte Darstellung einer Funktion durch die Menge ihrer Wertepaare (x, y), ihren Graphen. Der Graph der Funktion sagt zwar nicht mehr als tausend Worte, aber immerhin genausoviel wie die analytische Beschreibung.
Der Graph einer Funktion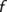 
ist die Menge aller Wertepaare
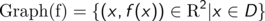
aufgefasst als Punkte der Ebene.
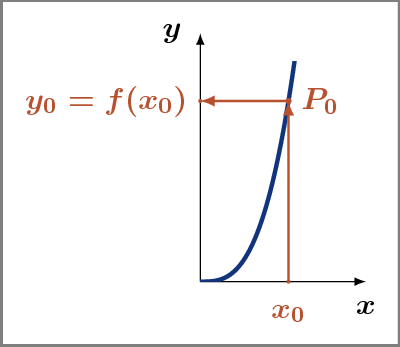
Den Graphen einer Funktion erhalten wir also wie folgt:
y0 = f(x0).
Die beschriebene punktweise Konstruktion eines Funktionsgraphen ist natürlich eine mühsame, meist wenig praktikable Vorgehensweise; sie diente uns in erster Linie dazu, das Konzept zu verstehen.
Geht das auch einfacher?
Klassisch: Kurvendiskussion
Modern: Funktionsplotter
Das klassische Mittel, eine Skizze des Graphen anzufertigen ist die Kurvendiskussion : man untersucht das Verhalten der Funktion im Unendlichen (d.h. für betragsmäßig sehr große Werte der unabhängigen Variablen), bestimmt die Nullstellen und Extremwerte (Maxima und Minima) sowie die Unendlichkeitsstellen (Polstellen).
Wenn man das ausreichend oft selber gemacht hat (also mindestens einmal), kann man heute auch auf spezielle Computerprogramme, sogenannte Funktionsplotter zurückgreifen, die aus der Funktionsvorschrift den Graphen erzeugen und so schnell einen Überblick über die allgemeinen Eigenschaften einer Funktion – Nullstellen, Extremwerte, Unendlichkeitsstellen, Steigungsverhalten, Krümmung, usw. – ermöglichen.
Funktionsplotter gibt es
