Wir haben nun ein Gefühl dafür, was Integrale sind und warum sie in Anwendungen auftreten. Fehlt noch, wie sie berechnet werden.
Eine äußerst schlagkräftige Methode zur Berechnung von Integralen liefert, quasi als Nebeneffekt, der Hauptsatz der Differential- und Integralrechnung. Er stellt einen, auf den ersten Blick ziemlich überraschenden, Zusammenhang zwischen Integrieren und Differenzieren her.
Für eine auf einem abgeschlossenem Intervall D = [a, b] stetige Funktion f gilt
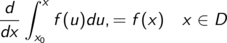
wobei x0 irgendein Punkt aus dem Intervall ist.
Ich gehe von einer stetigen Funktion f auf dem Intervall [a, b] aus, erhalte durch Integrieren mit variabler oberer Integrationsgrenze (bei fest gewählter unterer Integrationsgrenze x0) eine neue Funktion F
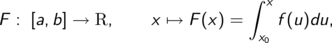
Differenzieren dieser “Integralfunktion” F führt dann genau wieder auf die Ausgangsfunktion f.
Es wird deutlich schwieriger. Bitte konsultieren Sie den Mathematiker Ihres Vertrauens oder schlagen in einem einschlägigen Mathematikbuch nach.
Lesen Sie die Sätze aber sehr sorgfältig. Beachten Sie insbesondere, was vorausgesetzt wird, also bei der Anwendung des Satzes im Einzelfall nachzuweisen ist. Das kann zum Beispiel die Integrierbarkeit von f sein.
Lassen wir zur Beantwortung dieser Frage kurz Betroffene zu Wort kommen